 |
 |
 |
 |
 |
Mathematics
To view our curriculum plans, please click the following:
Year 7 Year 8 Year 9 Year 10 Year 11 Year 12 Year 13
To view the Mathematics Department Feedback Policy, please click here.
Y6-7 Sparx Maths Transition Booklet – ANSWERS
ANSWERSTo view the answers as a PDF, please click here.
Welcome to the Mathematics Department!
Our belief:
Children’s chances of success are maximised if they develop
deep and lasting understanding of mathematical procedures and concepts.
Our Intent:
As a department we reject the idea that a large proportion of people ‘just can’t do maths’. All students and members of the St Hilda’s community are encouraged by the belief that by working hard at mathematics they can succeed and that making mistakes is to be seen not as a failure but as a valuable opportunity for new learning. The intent of our mathematics curriculum is to be accessible to all, maximising the development of every student’s ability and academic achievement. Challenge and the opportunity to deepen understanding of the key mathematical ideas is provided for all.
Maths is a journey and long-term goal, achieved through exploration, clarification, practice and application over time. We aim wherever possible to deliver lessons that are creative and engaging. We want children to make rich connections across mathematical ideas to develop fluency, mathematical reasoning and competence in solving increasingly sophisticated problems. At each stage of learning, children should be able to demonstrate a deep, conceptual understanding of the topic and be able to build on this over time.
As our students progress, we intend for them to be able to understand the world through the eyes of a mathematician and have an appreciation of the beauty and power of mathematics, and a sense of enjoyment and curiosity about the subject.
Extra Curricular Activites 2019-20



Our Implementation:
Mathematics is taught following the key principles of Mastery, using the five big ideas of Teaching for Mastery.
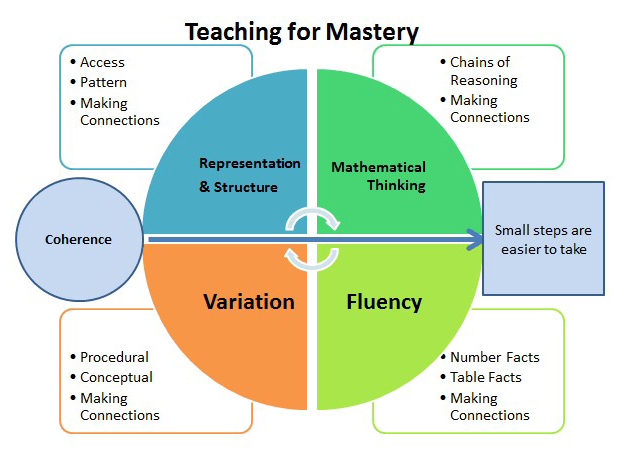
Differentiation
Decisions about progression are based on the security of pupils’ understanding and their readiness to progress to the next stage.
Every attempt is made to keep the whole class learning together. Differentiation is achieved, not through offering different content, but through adaptation, by paying attention to the levels of support and challenge needed to allow every student to fully grasp the concepts and ideas being studied. This ensures that all students gain sufficiently deep and secure understanding of the mathematics to form the foundation of future learning before moving to the next part of the curriculum sequence. This prevents students from being left behind. For those students who grasp ideas quickly, acceleration into new content is avoided. Instead, these students are challenged by deeper analysis of the lesson content and by applying the content in new and unfamiliar problem-solving situations and by being offered rich and sophisticated problems before any acceleration through new content. Those who are not sufficiently fluent are encouraged to consolidate their understanding, including through additional practice, before moving on. These students may receive additional support work to complete on-line or invited to attend Maths Clinic.
Intervention
If some students fail to grasp an important aspect of the lesson, this is identified quickly and early intervention ensures that they are ready to move forward with the whole class in the next lesson.
The following structure is followed for all new learning to ensure fluency and to ensure the identification of any necessary early intervention:
Teach → Assess → Feedback → Recall → Recall → Assessed recall
We recognise that there are 3 levels of learning:
- Shallow learning: surface, temporary, often lost
- Deep learning: it sticks, can be recalled and used
- Deepest learning: can be transferred and applied in different contexts
The deep and deepest levels are what we are aiming for by teaching maths using the Mastery approach and following this structure.
Revision Support
There are many resources available on the internet to help your child to revise for their mathematics exams. The school has subscribed to the following websites for your child:
www.mymaths.co.uk
www.vle.mathswatch.com
Your son/daughter has their own individual log-in details for these websites.
Students who require individual support are welcome to attend Maths Clinic:
Our Impact:
We will have succeeded when students become fluent in the fundamentals of mathematics, experiencing varied and frequent practice, encountering increasingly complex problems over time. Students will have developed conceptual understanding and the ability to recall and apply knowledge rapidly and accurately. Students will have mastered each mathematical concept or skill when they can show it in multiple ways, using the mathematical language to explain their ideas, and can independently apply the concept to new problems in unfamiliar situations. Students will have the ability to reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.
Oracy:
The Mathematics department support the whole school literacy policy in recognising the importance of spoken language in pupils’ development across the whole curriculum – cognitively, socially and linguistically. We believe that the quality and variety of language that pupils hear and speak are key factors in developing their mathematical vocabulary and presenting a mathematical justification, argument or proof. Teachers support students in making their thinking clear to themselves as well as others and teachers ensure that students build secure foundations by using discussion to probe and remedy their misconceptions.
Cross-curricular Maths:
We intend for our pupils to be able to apply their mathematical knowledge across all subjects. We want children to realise that mathematics has been developed over centuries, providing the solution to some of history’s most intriguing problems. We want them to know that it is essential to everyday life, critical to science, geography, computing, technology and engineering, and necessary for financial literacy and most forms of employment. Pupils are given the opportunity to become ‘Maths Spotters’ and identify when Maths is being used in other subjects. Maths Spotters award stickers to teachers that they can cash in for house points.
Key Stage 5
Intent
Our vision is for A-level maths classrooms to be vibrant places, where confident students, from different starting points, explore problems using mathematics, freely discuss and evaluate different approaches. They see the value of practice and personal study, and they work hard to produce high quality solutions and understand the ‘bigger picture’. Teacher explanations are incisive and clear, harnessing ICT to aid understanding. Teachers guide students in effective personal habits and model professional behaviours, communicating with students as ‘young adults’. Teachers and students are exam-focussed alongside a pursuit for deeper understanding. Learning is enriched through historical and ‘new’ mathematics and opportunities wide of the St Hilda’s classroom.
Entry criteria
Students are required to have achieved a grade 7 or above at GCSE to be able to enrol on Maths A-level at St Hilda’s and a grade 9 to enrol on Further Maths A-Level. During the A-level course we see students develop algebraic fluency that builds on critical components of the Higher Level GCSE such as indices, quadratics, proof and vectors.
The Mathematics Department follow the Pearson Edexcel A-Level Specification. The detailed specification is available at:
Where can MATHS take you?
MATHS

